Introduction
Frontend and backend
The POD2 system consists of a frontend and a backend, connected by a middleware. This page outlines some design principles for deciding which components go where.
user -- frontend -- middleware -- backend -- ZK circuit
The frontend is what we want the user to see; the backend is what we want the circuit to see.
Circuit and proving system
The first implementation of POD2 uses Plonky2 as its proving system. In principle, a future implementation could use some other proving system. The frontend and middleware should not be aware of what proving system is in use: anything specific to the proving system belongs to the backend.
User-facing types versus in-circuit types
The frontend type system exposes human-readable types to POD developers: strings, ints, bools, and so forth. On the backend, all types are build out of field elements. The middleware should handle the conversion.
POD value types
From the frontend perspective, POD values may be one of the following1 types: four atomic types
IntegerBoolStringRaw
and three compound types
DictionaryArraySet.
From the backend perspective, however, these types will all be encoded as a fixed number of field elements, the number being chosen so as to accommodate the Integer type as well as hashes to represent the String and compound types with the appropriate level of security.
In the case of the Plonky2 backend with 100 bits of security, all of these types are represented as 4 field elements, the output of the Poseidon hash function used there being
Integer
In the frontend, this type is none other than u642. In the backend, it will be appropriately embedded into the codomain of the canonical hash function.
Bool
In the frontend, this is a simple bool. In the backend, it will have the same encoding as an Integer 0 (for false) or 1 (for true).
String
In the frontend, this type corresponds to the usual String. In the backend, the string will be mapped to a sequence of field elements and hashed with the hash function employed there, thus being represented by its hash.
Raw
"Raw" is short for "raw value". A Raw exposes a backend Value on the frontend.
With the plonky2 backend, a Raw is a tuple of 4 elements of the Goldilocks field.
Dictionary, array, set
The array, set and dictionary types are similar types. While all of them use a merkletree under the hood, each of them uses it in a specific way:
- dictionary: the user original keys and values are hashed to be used in the leaf.
leaf.key=hash(original_key)leaf.value=hash(original_value)
- array: the elements are placed at the value field of each leaf, and the key field is just the array index (integer)
leaf.key=ileaf.value=original_value
- set: both the key and the value are set to the hash of the value.
leaf.key=hash(original_value)leaf.value=hash(original_value)
In the three types, the merkletree under the hood allows to prove inclusion & non-inclusion of the particular entry of the {dictionary/array/set} element.
A concrete implementation of dictionary, array, set can be found at pod2/src/middleware/containers.rs.
TODO In POD 1, there is the cryptographic type, which has the same type of the output of the hash function employed there. It is useful for representing arbitrary hashes. Do we want to expand our type list to include a similar type, which would correspond to the HashOut type in the case of Plonky2? This would not have a uniform representation in the frontend if we continue to be backend agnostic unless we fix the number of bits to e.g. 256, in which case we would actually need one more field element in the case of Plonky2.
TODO Replace this with i64 once operational details have been worked out.
Anchored keys
Rather than dealing with just keys, we introduce the notion of an anchored key, which is a pair consisting of an dictionary specifier and a key, i.e.
type AnchoredKey = (Dict, Key)
type Key = String
Statements can use anchored keys or literal values as arguments. Since our
system uses constructive logic, if a statement that uses an anchored key in
some of its arguments is proved, it means that a valid Merkle proof of the
value behind it exists and was used at some point to construct a Contains
statement that introduced that anchored key.
In PODLang, anchored key indexing can use subscript syntax foo["bar"] which
allows any string key, or dot syntax foo.bar if the key is a valid identifier.
For example:
0: None
1: Contains(foo, "bar", 42) <- ContainsFromEntries 0 0 0 mt_proof
2: Lt(foo["bar"], 100) <- LtFromEntries 1 0
3: NotEqual(foo.bar, 100) <- LtToNotEqual 2
Backend types
On the backend, there is only a single type: Value.
A Value is simply a tuple of field elements. With the plonky2 backend, a Value is a tuple of 4 field elements. In general, the backend will expose a constant VALUE_SIZE, and a Value will be a tuple of VALUE_SIZE field elements.
Integers and booleans
The backend encoding stores integers in such a way that arithmetic operations (addition, multiplication, comparison) are inexpensive to verify in-circuit.
In the case of the Plonky2 backend, an integer is decomposed as with and represented as where is the canonical projection.
On the backend, a boolean is stored as an integer, either 0 or 1; so logical operations on booleans are also inexpensive.
Strings
The backend encoding stores strings as hashes, using a hash function that might not be zk-friendly. For this reason, string operations (substrings, accessing individual characters) are hard to verify in-circuit. The POD2 system does not provide methods for manipulating strings.
In other words: As POD2 sees it, two strings are either equal or not equal. There are no other relationships between strings.
In the case of the Plonky2 backend, a string is converted to a sequence of bytes with the byte 0x01 appended as padding, then the bytes are split into 7-byte chunks starting from the left, these chunks then being interpreted as integers in little-endian form, each of which is naturally an element of GoldilocksField, whence the resulting sequence may be hashed via the Poseidon hash function. Symbolically, given a string , its hash is defined by
where poseidon is the Poseidon instance used by Plonky2, is as above, is defined such that[^aux]
the mapping is given by
and is the canonical mapping of a string to its UTF-8 representation.
Compound types
The three front-end compound types (Dictionary, Array, Set) are all represented as Merkle roots on the backend. The details of the representation are explained on a separate Merkle tree page.
MerkleTree
In the POD2 backend, a MerkleTree is used to store an unordered set of key-value pairs. The frontend compound types Array, Set, and Dictionary are all represented as MerkleTrees on the backend.
From the high level, we can think of a MerkleTree as a 'hashmap' storage, that allows us to generate proofs of inclusion and non-inclusion of the key-values stored into it.
A MerkleTree is represented in-circuit as its Merkle root; in the Plonky2 backend, this root is a tuple of four field elements. This makes a MerkleTree the same size in-circuit as the atomic types Integer and String. (In general, regardless of the proof system used on the backend, all three types are represented in-circuit by the same number of field elements; this number is determined by the security requirement of the hash function.)
The encoding of the MerkleTree is a recursive process:
- Encode all keys and values in the
MerkleTree. - Put all keys and values into a sparse Merkle tree.
- The
MerkleTreeis encoded in-circuit as the root of this sparse Merkle tree.
This document explains the construction of the sparse Merkle tree.
The branching rule
A sparse Merkle tree is implemented as a binary tree. The insertion path of any key is given by a deterministic rule: given key and a nonnegative integer depth, the rule determines that key belongs to either the left or right branch at depth depth.
The precise rule is as follows. In-circuit, compute a Poseidon hash of key to obtain a 4-tuple of field elements
Poseidon(key) = (k_0, k_1, k_2, k_3).
Write the field elements in binary (in little-endian order):
k_0 = b_0 b_1 ... b_63
k_1 = b_64 b_65 ... b_127
....
At the root, key goes to the left subtree if b_0 = 0, otherwise the right subtree. At depth 1, key goes to the left subtree if b_1 = 0, otherwise the right subtree, and similarly for higher depth.
The tree structure
A Merkle tree with no entry at all is represented by the hash value
root = hash(0).
(With the Plonky2 backend, the hash function hash will output a 4-tuple of field elements.)
A Merkle tree with a single entry (key, value) is called a "leaf". It is represented by the hash value
root = hash(1, (key, value)), where 1 is a flag indicating that it is a leaf, and it's used as the initial state of the hash (Poseidon) permutation.
A Merkle tree tree with more than one entry is required to have two subtrees, left and right. It is then represented by the hash value
root = hash(2, (left_root, right_root)), where 2 is a flag indicating that it is an intermediate node, and it's used as the initial state of the hash (Poseidon) permutation.
The flags are used as the initial state of the Poseidon permutation so that they don't account for extra inputs in the Poseidon gadget, needing only 1 gate for each node/leaf hash.
(The role of the constants 1 and 2 is to prevent collisions between leaves and non-leaf Merkle roots. If the constants were omitted, a large Merkle tree could be dishonestly interpreted as a leaf, leading to security vulnerabilities.)
Example 1
Suppose we want to build a Merkle tree from the following Dictionary with three key-value pairs:
{
4: "even",
5: "odd",
6: "even"
}
The keys are integers, so the are represented in-circuit by themselves. Let's suppose that in little-endian order, the first three bits of the hashes of the keys are:
hash(4) = 000...
hash(5) = 010...
hash(6) = 001...
The resulting tree looks like:
root
/\
/ \
/ \
/ \
L_root R_root = hash(0)
/\
/ \
/ \
/ \
LL_root LR_root = hash((4, "even", 1))
/\
/ \
/ \
/ \
LLL_root LLR_root = hash((5, "odd", 1))
||
hash((6, "even", 1))
The intermediate roots are computed as hashes of their subroots:
LL_root = hash((LLL_root, LLR_root, 2))
L_root = hash((LL_root, LR_root, 2))
root = hash((L_root, R_root, 2)).
The full Dictionary is then represented in the backend as root (four field elements in the Plonky2 backend).
Example 2
So for example, imagine we have 8 key-pairs, where the keys are just an enumeration from 0 to 7, then the tree leaves positions would look like:
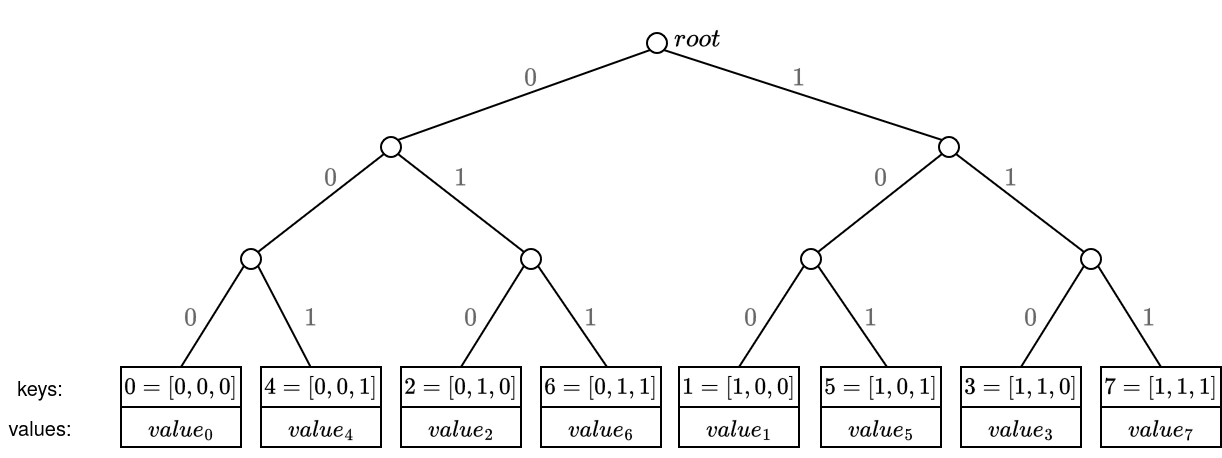
Now let's change the key of the leaf key=1, and set it as key=13. Then, their respective leaf paths will be the same until they diverge in the 4-th bit:
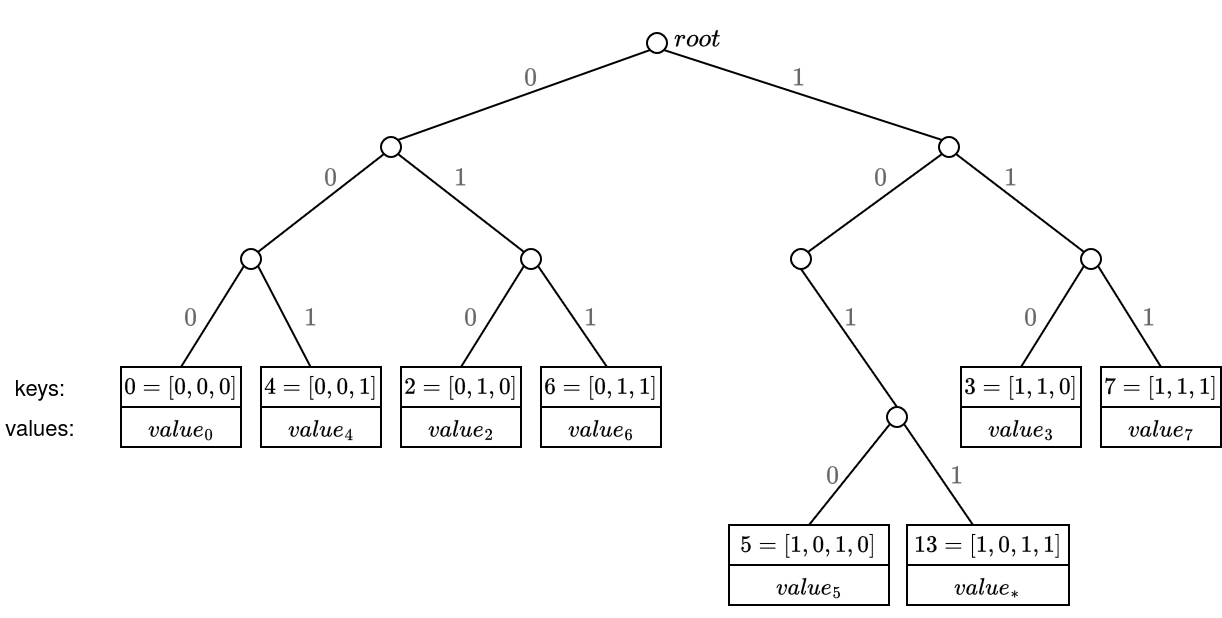
Example 3
Suppose we have 4 key-values, where the first four bits of the hashes of the keys are 0000, 0100, 1010 and 1011. The tree would look like:
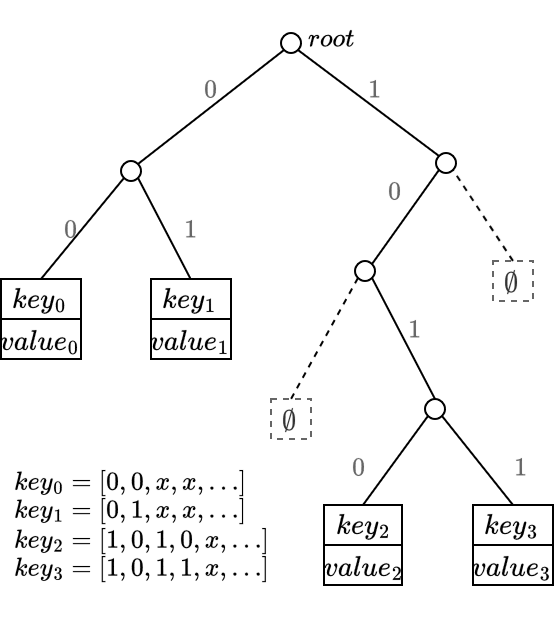
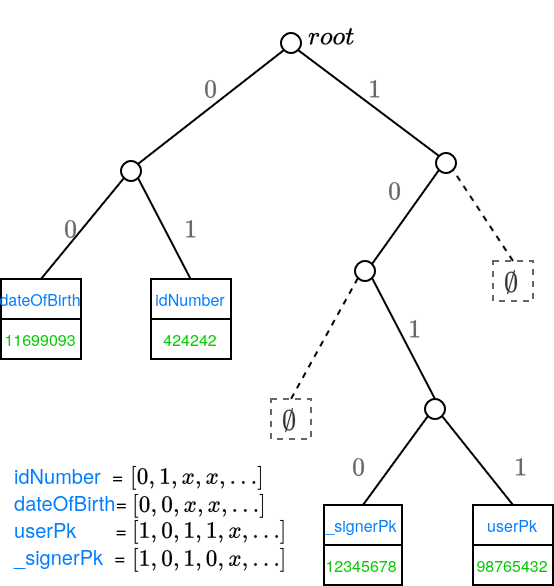
To iterate this example, suppose we have the following data in a POD:
{
id: "11000...",
kvs : {
idNumber: "424242",
dateOfBirth: 1169909384,
userPk: 9876543210, // target user of this POD
_signerPk: 1234567890, // signer of the POD
},
// ...
}
The merkletree will contain the key values from the kvs field.
Suppose that the binary representation of the hash of the key userPk is 1011.... This uniquely defines the leaf position that contains the public key of the authenticated user. Similarly for the other key-values:
Proofs of inclusion and non-inclusion
Merkle proofs contain the siblings along the path from the leaf to the root, where the leaf position is determined by the key binary representation.
Since leaf positions are deterministic based on the key, the same approach is used for non-inclusion proofs, where it can be proven that a key is not in the tree, and furthermore, that a value is not in the tree (although the key exists):
- Proving that the key does not exist in the tree is achieved by generating the merkle-proof for the specific key, and showing that the (virtual) leaf is empty - this is, showing that going down the path of the non-existing key, there is a leaf with a different key, meaning that the non-existing key has not been inserted in the tree.
- Proving that a value is not in the tree (although the key exists) is achieved by generating the merkle-proof for the specific key, and showing that the leaf exists but it has a different value than the one being proved.
For the current use cases, we don't need to prove that the key exists but the value is different on that leaf, so we only use the option 1.
There are 2 cases to have into account when dealing with non-inclusion proofs:
- case i) the expected leaf does not exist.
- case ii) the expected leaf does exist in the tree, but it has a different
key.
Encoding
TODO: how key-values, nodes, merkle-proofs, ... are encoded.
Interface
#![allow(unused)] fn main() { impl MerkleTree { /// builds a new `MerkleTree` where the leaves contain the given key-values fn new(max_depth: usize, kvs: &HashMap<Value, Value>) -> Result<Self>; /// returns the root of the tree fn root(&self) -> Hash; /// returns the max_depth parameter from the tree fn max_depth(&self) -> usize; /// returns the value at the given key fn get(&self, key: &Value) -> Result<Value>; /// returns a boolean indicating whether the key exists in the tree fn contains(&self, key: &Value) -> Result<bool>; /// returns a proof of existence, which proves that the given key exists in /// the tree. It returns the `value` of the leaf at the given `key`, and the /// `MerkleProof`. fn prove(&self, key: &Value) -> Result<(Value, MerkleProof)>; /// returns a proof of non-existence, which proves that the given /// `key` does not exist in the tree. The return value specifies /// the key-value pair in the leaf reached as a result of /// resolving `key` as well as a `MerkleProof`. fn prove_nonexistence(&self, key: &Value) -> Result<MerkleProof>; /// verifies an inclusion proof for the given `key` and `value` fn verify(max_depth: usize, root: Hash, proof: &MerkleProof, key: &Value, value: &Value,) -> Result<()>; /// verifies a non-inclusion proof for the given `key`, that is, the given /// `key` does not exist in the tree fn verify_nonexistence( max_depth: usize, root: Hash, proof: &MerkleProof, key: &Value,) -> Result<()>; /// returns an iterator over the leaves of the tree fn iter(&self) -> Iter; } }
Development plan
- short term: merkle tree as a 'precompile' in POD operations, which allows to directly verify proofs
- long term exploration:
- explore feasibility of using Starky (for lookups) connected to Plonky2, which would allow doing the approach described at https://hackmd.io/@aardvark/SkJ-wcTDJe
Resources
Signature
For POD2 signatures, we use Schnorr signature over the EcGFp5 curve.
Older version
The previously used signature scheme was proof-based signatures using Plonky2 proofs, following https://eprint.iacr.org/2024/1553 and https://jdodinh.io/assets/files/m-thesis.pdf. This came from Polygon Miden's RPO STARK-based signatures.
This was replaced by the elliptic curve Schnorr signature presented above, keeping the description here in case it were useful in the future.
The scheme was as follows:
generate_params()
: plonky2 circuit prover params
: plonky2 circuit verifier params
return
keygen()
secret key:
public key: 1
return
sign(pp, sk, m)
return
verify(vp, sig, pk, m)
return
Plonky2 circuit
private inputs:
public inputs:
The 2024/1553 paper uses to have as input (to the hash) 8 field elements, to be able to reuse the same instance of the RPO hash as the one they use later in the signature (where it hashes 8 field elements).
Deductions
Statements
A statement is any sort of claim about the values of entries: for example, that two values are equal, or that one entry is contained in another.
Statements come in two types: built-in and custom. There is a short list of built-in statements (see below). 1 In addition, users can freely define custom statements.
From the user (front-end) perspective, a statement represents a claim about the values of some number of entries -- the statement can only be proved if the claim is true. On the front end, a statement is identified by its name (ValueOf, Equal, etc.).
From the circuit (back-end) perspective, a statement can be proved either:
- by direct in-circuit verification, or
- by an operation (aka deduction rule). On the back end, a statement is identified by a unique numerical identifier.
Built-in statements
The POD system has several builtin statements. These statements are associated to a reserved set of statement IDs.
Backend statements
A statement is a code (or, in the frontend, string identifier) followed by 0 or more arguments. These arguments may consist of up to three anchored keys and up to one POD value.
The following table summarises the natively-supported statements, where we write value_of(ak) for 'the value anchored key ak maps to', which is of type PODValue, and key_of(ak) for the key part of ak:
| Code | Identifier | Args | Meaning |
|---|---|---|---|
| 0 | None | no statement, always true (useful for padding) | |
| 1 | False | always false (useful for padding disjunctions) | |
| 2 | Equal | ak1, ak2 | value_of(ak1) = value_of(ak2) |
| 3 | NotEqual | ak1, ak2 | value_of(ak1) != value_of(ak2) |
| 4 | LtEq | ak1, ak2 | value_of(ak1) <= value_of(ak2) |
| 5 | Lt | ak1, ak2 | value_of(ak1) < value_of(ak2) |
| 6 | Contains | ak1, ak2, ak3 | (value_of(ak2), value_of(ak3)) ∈ value_of(ak1) (Merkle inclusion) |
| 7 | NotContains | ak1, ak2 | (value_of(ak2), _) ∉ value_of(ak1) (Merkle exclusion) |
| 8 | SumOf | ak1, ak2, ak3 | value_of(ak1) = value_of(ak2) + value_of(ak3) |
| 9 | ProductOf | ak1, ak2, ak3 | value_of(ak1) = value_of(ak2) * value_of(ak3) |
| 10 | MaxOf | ak1, ak2, ak3 | value_of(ak1) = max(value_of(ak2), value_of(ak3)) |
| 11 | HashOf | ak1, ak2, ak3 | value_of(ak1) = hash(value_of(ak2), value_of(ak3)) |
| 12 | PublicKeyOf | ak1, ak2 | value_of(ak1) = derive_public_key(value_of(ak2)) |
| 13 | SignedBy | ak1, ak2 | value_of(ak1) is signed by value_of(ak2) |
| 14 | ContainerInsert | ak1, ak2, ak3, ak4 | (value_of(ak3), _) ∉ value_of(ak2) ∧ value_of(ak1) = value_of(ak2) ∪ {(value_of(ak3), value_of(ak4))} (Merkle insert) |
| 15 | ContainerUpdate | ak1, ak2, ak3, ak4 | (value_of(ak3), v) ∈ value_of(ak2) ∧ value_of(ak1) = (value_of(ak2) - {(value_of(ak3), v)}) ∪ {(value_of(ak3), value_of(ak4))} (Merkle update) |
| 16 | ContainerDelete | ak1, ak2, ak3 | (value_of(ak3), v) ∈ value_of(ak2) ∧ value_of(ak1) = value_of(ak2) - {(value_of(ak3), v)} (Merkle delete) |
Frontend statements
The frontend also exposes the following syntactic sugar predicates. These predicates are not supported by the backend. The frontend compiler is responsible for translating these predicates into the predicates above.
| Code | Identifier | Args and desugaring |
|---|---|---|
| 1000 | DictContains | DictContains(root, key, val) -> Contains(root, key, val) |
| 1001 | DictNotContains | DictNotContains(root, key) -> NotContains(root, key) |
| 1002 | SetContains | SetContains(root, val) -> Contains(root, val, val) |
| 1003 | SetNotContains | SetNotContains(root, val) -> Contains(root, val, val) |
| 1004 | ArrayContains | ArrayContains(root, idx, val) -> Contains(root, idx, val) |
| 1005 | GtEq | GtEq(a, b) -> LtEq(b, a) |
| 1006 | Gt | Gt(a, b) -> Lt(b, a) |
| 1009 | DictInsert | DictInsert(new_root, old_root, key, val) -> ContainerInsert(new_root, old_root, key, val) |
| 1010 | DictUpdate | DictUpdate(new_root, old_root, key, val) -> ContainerUpdate(new_root, old_root, key, val) |
| 1011 | DictDelete | DictDelete(new_root, old_root, key) -> ContainerDelete(new_root, old_root, key) |
| 1012 | SetInsert | SetInsert(new_root, old_root, val) -> ContainerInsert(new_root, old_root, val, val) |
| 1013 | SetDelete | SetDelete(new_root, old_root, val) -> ContainerDelete(new_root, old_root, val) |
| 1014 | ArrayUpdate | ArrayUpdate(new_root, old_root, idx, val) -> ContainerUpdate(new_root, old_root, idx, val) |
Built-in statements for entries of any type
A DictContains statement asserts that an entry has a certain value.
DictContains(A, "name", "Arthur")
Implies that the entry A["name"] exists with the value "Arthur".
An Equal statement asserts that two entries have the same value. (Technical note: The circuit only proves equality of field elements; no type checking is performed. For strings or Merkle roots, collision-resistance of the hash gives a cryptographic guarantee of equality. However, note both Arrays and Sets are implemented as dictionaries in the backend; the backend cannot type-check, so it is possible to prove an equality between an Array or Set and a Dictionary.)
Equal(A["name"], B["name"])
An NotEqual statement asserts that two entries have different values.
NotEqual (for arbitrary types)
Built-in Statements for Numerical Types
An Gt(x, y) statement asserts that x is an entry of type Integer, y is an entry or constant of type Integer, and x > y.
Gt (for numerical types only)
Gt(A["price"], 100)
Gt(A["price"], B["balance"])
The statements Lt, GEq, Leq are defined analogously.
SumOf(x, y, z) asserts that x, y, z are entries of type Integer, and x = y + z
ProductOf and MaxOf are defined analogously.
The two items below may be added in the future:
poseidon_hash_of(A["hash"], B["preimage"]) // perhaps a hash_of predicate can be parametrized by an enum representing the hash scheme; rather than having a bunch of specific things like SHA256_hash_of and poseidon_hash_of etc.
ecdsa_priv_to_pub_of(A["pubkey"], B["privkey"])
TODO List of built-in statements is not yet complete.
Operations
The mechanism by which statements are derived is furnished by operations. Roughly speaking, with few exceptions, an operation deduces a statement from one or more existing statements according to some relation that must be satisfied between these statements. For example, if Equal(ak1, ak2) holds true, then the operation SymmetricEq applied to this statement yields Equal(ak2, ak1).
More precisely, an operation is a code (or, in the frontend, string identifier) followed by 0 or more arguments. These arguments may consist of up to three statements, up to one key-value pair and up to one Merkle proof.
The following table summarises the natively-supported operations:
| Code | Identifier | Args | Condition | Output |
|---|---|---|---|---|
| 0 | None | None | ||
| 1 | CopyStatement | s | ||
| 2 | EqualFromEntries | s1, s2 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), value1 = value2 | Equal(ak1, ak2) |
| 3 | NotEqualFromEntries | s1, s2 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), value1 != value2 | NotEqual(ak1, ak2) |
| 4 | LtEqFromEntries | s1, s2 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), value1 <= value2 | LtEq(ak1, ak2) |
| 5 | LtFromEntries | s1, s2 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), value1 < value2 | Lt(ak1, ak2) |
| 6 | TransitiveEqualFromStatements | s1, s2 | s1 = Equal(ak1, ak2), s2 = Equal(ak3, ak4), ak2 = ak3 | Equal(ak1, ak4) |
| 7 | LtToNotEqual | s | s = Lt(ak1, ak2) | NotEqual(ak1, ak2) |
| 8 | ContainsFromEntries | s1, s2, s3, proof | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), merkle_includes(value1, value2, value3, proof) = true | Contains(ak1, ak2, ak3) |
| 9 | NotContainsFromEntries | s1, s2, proof | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), merkle_excludes(value1, value2, proof) = true | NotContains(ak1, ak2) |
| 10 | SumOf | s1, s2, s3 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), value1 = value2 + value3 | SumOf(ak1, ak2, ak3) |
| 11 | ProductOf | s1, s2, s3 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), value1 = value2 * value3 | ProductOf(ak1, ak2, ak3) |
| 12 | MaxOf | s1, s2, s3 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), value1 = max(value2, value3) | MaxOf(ak1, ak2, ak3) |
| 13 | HashOf | s1, s2, s3 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), value1 = hash(value2, value3) | HashOf(ak1, ak2, ak3) |
| 14 | PublicKeyOf | s1, s2 | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), value1 = derive_public_key(value2) | PublicKeyOf(ak1, ak2) |
| 15 | SignedBy | s1, s2, sig | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), verify_signature(msg: value1, pk: value2, sig) = true | SignedBy(ak1, ak2) |
| 16 | ContainerInsertFromEntries | s1, s2, s3, s4, proof | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), s4 = Contains(ak4..., value4), merkle_insert(value1, value2, value3, value4, proof) = true | ContainerInsert(ak1, ak2, ak3, ak4) |
| 17 | ContainerUpdateFromEntries | s1, s2, s3, s4, proof | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), s4 = Contains(ak4..., value4), merkle_update(value1, value2, value3, value4, proof) = true | ContainerUpdate(ak1, ak2, ak3, ak4) |
| 18 | ContainerDeleteFromEntries | s1, s2, s3, proof | s1 = Contains(ak1..., value1), s2 = Contains(ak2..., value2), s3 = Contains(ak3..., value3), merkle_delete(value1, value2, value3, proof) = true | ContainerDelete(ak1, ak2, ak3, ak4) |
The following table summarizes "syntactic sugar" operations. These operations are not supported by the backend. The frontend compiler is responsible for translating these operations into the operations above.
| Code | Identifier | Args and desugaring |
|---|---|---|
| 1001 | DictContainsFromEntries | DictContainsFromEntries(dict_st, key_st, value_st, proof_st) -> ContainsFromEntries(dict_st, key_st, value_st, proof_st) |
| 1002 | DictNotContainsFromEntries | DictNotContainsFromEntries(dict_st, key_st, proof_st) -> NotContainsFromEntries(dict_st, key_st, proof_st) |
| 1003 | SetContainsFromEntries | SetContainsFromEntries(set_st, value_st, proof_st) -> ContainsFromEntries(set_st, value_st, value_st, proof_st) |
| 1004 | SetNotContainsFromEntries | SetNotContainsFromEntries(set_st, value_st, proof_st) -> NotContainsFromEntries(set_st, value_st, value_st, proof_st) |
| 1005 | ArrayContainsFromEntries | ArrayContainsFromEntries(array_st, index_st, value_st, proof_st) -> ContainsFromEntries(array_st, index_st, value_st, proof_st) |
| 1006 | GtEqFromEntries | GtEqFromEntries(s1, s2) -> LtEqFromEntries(s2, s1) |
| 1007 | GtFromEntries | GtFromEntries(s1, s2) -> LtFromEntries(s2, s1) |
| 1008 | GtToNotEqual | GtToNotEqual(s1, s2) -> LtToNotEqual(s1, s2) |
| 1009 | DictInsertFromEntries | DictInsertFromEntries(new_dict_st, old_dict_st, key_st, value_st, proof) -> ContainerInsertFromEntries(new_dict_st, old_dict_st, key_st, value_st, proof) |
| 1010 | DictUpdateFromEntries | DictInsertUpdateEntries(new_dict_st, old_dict_st, key_st, value_st, proof) -> ContainerUpdateFromEntries(new_dict_st, old_dict_st, key_st, value_st, proof) |
| 1011 | DictDeleteFromEntries | DictInsertDeleteEntries(new_dict_st, old_dict_st, key_st, proof) -> ContainerDeleteFromEntries(new_dict_st, old_dict_st, key_st, value_st, proof) |
| 1009 | SetInsertFromEntries | SetInsertFromEntries(new_set_st, old_set_st, value_st, proof) -> ContainerInsertFromEntries(new_set_st, old_set_st, value_st, value_st, proof) |
| 1011 | SetDeleteFromEntries | SetInsertDeleteEntries(new_set_st, old_set_st, value_st, proof) -> ContainerDeleteFromEntries(new_set_st, old_set_st, value_st, value_st, proof) |
| 1010 | ArrayUpdateFromEntries | ArrayInsertUpdateEntries(new_array_st, old_array_st, index_st, value_st, proof) -> ContainerUpdateFromEntries(new_array_st, old_array_st, index_st, value_st, proof) |
WIP. The following table defines more operations that are not yet implemented.
Issue keeping track of the operations: #108.
| Code | Identifier | Args | Condition | Output |
|---|---|---|---|---|
SymmetricEq | s | s = Equal(ak1, ak2) | Eq(ak2, ak1) | |
SymmetricNEq | s | s = NotEqual(ak1, ak2) | NEq(ak2, ak1) | |
RenameSintains | s1, s2 | s1 = Sintains(ak1, ak2), s2 = Equal(ak3, ak4), ak1 = ak3 | Sintains(ak4, ak2) | |
TransitiveEq | s1, s2 | s1 = Equal(ak1, ak2), s2 = Equal(ak3, ak4), ak2 = ak3 | Eq(ak1, ak4) | |
TransitiveGt | s1, s2 | s1 = Gt(ak1, ak2), s2 = Gt(ak3, ak4), ak2 = ak3 | Gt(ak1, ak4) | |
TransitiveLEq | s1, s2 | s1 = LEq(ak1, ak2), s2 = LEq(ak3, ak4), ak2 = ak3 | LEq(ak1, ak4) | |
LEqToNEq | s | s = LEq(ak1, ak2) | NEq(ak1, ak2) |
Simple example
Circuit structure, two-column proof
A "proof" is a table that looks like
| STATEMENT | REASON |
|---|---|
| STATEMENT1 | REASON1 |
| STATEMENT2 | REASON2 |
| ... |
In other words:
A "proof" is an ordered list of 100 proof-rows.
Each "row" is a pair (statement, reason).
The statement is the statement.
The reason is everything the circuit needs to verify that the statement is true.
Example:
STATEMENT1 = Equals(olddict["name"], otherdict["field"])
STATEMENT2 = Equals(otherdict["field"], newdict["result"])
STATEMENT3 = Equals(olddict["name"], newdict["result"])
The reasons in human-readable simplified format:
REASON1 -- "came from previous pod"
REASON2 -- "came from previous pod"
REASON3 -- "use transitive property on STATEMENT1 and STATEMENT2"
What does the reason look like in circuit?
It won't be so simple. I'll just explain what REASON3 has to look like.
First, the operation (deduction rule).
A simple example of a deduction rule
Here is the transitive property of equality, in human-readable form.
if
Equals(a, b) and Equals(b, c)
then
Equals(a, c)
First, we need to decompose all the anchored keys as (dict, key) pairs. This is the frontend description of the deduction rule.
IF
Equals(a_or[a_key], b_or[b_key])
AND
Equals(b_or[b_key], c_or[c_key])
THEN
Equals(a_or[a_key], c_or[c_key])
In-circuit, all these identifiers are replaced with wildcards, which come in numerical order (because they will be used as array indices). So the backend representation is:
IF
Equals( ?1[?2], ?3[?4] ) and Equals ( ?3[?4], ?5[?6] )
THEN
Equals( ?1[?2], ?5[?6] )
What does REASON3 need to look like in-circuit?
- Repeat deduction rule
IF
Equals( ?1[?2], ?3[?4] ) and Equals ( ?3[?4], ?5[?6] )
THEN
Equals( ?1[?2], ?5[?6] )
- Say what the wildcards are
?1 -- olddict
?2 -- "name"
?3 -- otherdict
...
- Substitute the wildcards into the deduction rule
IF
Equals( olddict["name"], ... ) ...
Equals( otherdict["value"])
THEN
Equals( olddict["name"] newdict[...] )
...
- Say where to find the previous statements (indices in the list), and check that they are above this one.
Statement1
Statement2
- Check that the input statements match. Check that the output statement matches.
Decomposing anchored keys
Sometimes a deduction rule requires different anchored keys to come from the same dictionary. Here's an example from Ethdos.
The wildcard system handles this very naturally, since the dict of the anchored key can use its own wildcard.
eth_friend(src_or, src_key, dst_or, dst_key) = and<
// the attestation dict is signed by (src_or, src_key)
SignedBy(attestation_dict, src_or[src_key])
// that same attestation pod has an "attestation"
Equal(attestation_dict["attestation"], dst_or[dst_key])
>
In terms of anchored keys, it would be a little more complicated. five anchored keys show up in this deduction rule:
AK1 = src
AK2 = dst
AK3 = attestation_dict["attestation"]
and we need to force AK3, AK4, AK5 to come from the same origin.
WILDCARD matching takes care of it.
eth_friend(?1, ?2, ?3, ?4) = and<
// the attestation dict is signed by (src_or, src_key)
SignedBy(?5, ?1[?2])
// that same attestation pod has an "attestation"
Equal(?5["attestation"], ?3[?4])
>
Another perspective
When working with statements and operations, it might be useful to see them from another perspective:
- A predicate is a relation formula, which when filled with values becomes a statement.
- A statement can be seen as the constraints of a traditional zk-circuit, which can be true or false.
- An operation comprises the deduction rules, which are rules used to deduce new statements from previous statements or used to construct new statements from values.
For example,
Equalfor integers is a predicatest_1 = Equal(A, B)is a statementst_2 = Equal(B, C)is a statementst_3 = TransitiveEqualFromStatements(st_1, st_2)is an operation, which yields the statementst_3 = Equal(A, C)
So, for example, for the given predicate:
IsComposite(n, private: a, b) = AND(
ProductOf(n, a, b)
GtFromEntries(a, 1)
GtFromEntries(b, 1)
)
We can view it as:
The statement IsComposite(n) is true if and only if n, a, b
such that the following statements hold:
Custom statements and custom operations
Users of the POD system can introduce custom predicates (previously called custom statements) to express complex logical relations not available in the built-in predicates. Every custom predicate is defined as the conjunction (AND) or disjunction (OR) of a small number of other statements.
When a custom predicate is introduced in a MainPod, it becomes available for use in that POD and all PODs that inherit1 from it.
On the frontend, a custom predicate is defined as a collection of conjunctions and disjunctions of statements. The definition can be recursive: the definition of a predicate can involve the predicate itself, or the definitions of several predicates can depend on each other.
At the backend level, every definition of a predicate is either a conjunction or a disjunction of statements. To convert a frontend custom predicate to the backend, the middleware may need to introduce sub-predicates.
On the backend, custom predicates are defined in groups. A group can contain one or more custom predicates and their associated sub-predicates. Recursive definition is only possible within a group: the definition of a predicate in a group can only depend on previously existing predicates, itself, and other predicates in the same group.
Arguments of custom predicates
The definition of a custom predicate might also be called an operation or deduction rule. It includes two (or, potentially, say, five) statement templates as conditions. The arguments to the statement templates are decomposed as (origin, key) pairs: if statements are allowed to have arity at most 4, then the statement templates in a deduction rule will have at most 8 arguments (4 origins and 4 keys). The same holds for the output statement.
Each argument (origin or key) to an statement template is either a wildcard or a literal. In the backend, the wildcard arguments will be identified as ?1, ?2, ?3, ....
Examples
See examples
Hashing and predicate IDs
Each custom predicate is defined as part of a group of predicates. The definitions of all statements in the group are merklelized (using sequential indices as keys) (see examples) and the root of the merkle tree is used as the identifier. For more details, see the pages on hashing custom statements and custom predicates.
How to prove an application of an operation
The POD proof format is inspired by "two-column proofs" (for an example, see Wikipedia). A POD contains a "tabular proof", in which each row includes a "statement" and an "operation". The "operation" is the "reason" that justifies the statement: it is everything the circuit needs as a witness to verify the statement.
For a custom statement, the "reason" includes the following witnesses and verifications:
- the definition of the statement, serialized (see examples)
- if the statement is part of a group, the definition of the full group, serialized
- verify that the hash of the definition is the statement ID
- the definition will have some number of "wildcards" (?1, ?2, ...) as arguments to statement templates; a value for each wildcard must be provided as a witness (each will be either an origin ID or key)
- the circuit must substitute the claimed values for the wildcards, and the resulting statements (true statements with origins and keys) will appear as witnesses
- the circuit must verify that all the input statement templates (with origins and keys) appear in the previous statements (in higher rows of the table)
- the circuit also substitutes the claimed values for the wildcards in the output statement, and verifies that it matches the claimed output statement
What to call this? One POD "inherits" from another?
Defining custom predicates
(Note: At the moment, we consider a "custom operation" to be exactly the same thing as the "definition of a custom predicate.")
A custom operation 1 is a rule that allows one to deduce a custom statement from one or more existing statements according to a logical rule, described below.
Note: Unlike built-in operations, it is not possible to perform arbitrary calculations inside a custom operation.
The syntax of a custom operation is best explained with an example.
Original example with anchored keys, origins, and keys.
| Args | Condition | Output |
|---|---|---|
| signed_dict: Dict, signer: PublicKey, good_boy_issuers: AnchoredKey::MerkleRoot, receiver: AnchoredKey | SignedBy(signed_dict, signer), Contains(good_boy_issuers, signer), Equals(signed_dict["friend"], receiver) | GoodBoy(receiver, good_boy_issuers) |
Compiled example with only origins and keys.
| Args | Condition | Output |
|---|---|---|
| signed_dict: Dict, signer: PublicKey, good_boy_issuers_origin: Origin, good_boy_issuers_key: Key::MerkleRoot, receiver_origin: Origin, receiver_key: Key | SignedBy(signed_dict, signer), Contains(good_boy_issuers_origin[good_boy_issuers_key], signer), Equals(signed_dict["friend"], receiver_origin[receiver_key]) | GoodBoy(receiver_origin[receiver_key]), good_boy_issuers_origin[good_boy_issuers_key]) |
A custom operation accepts as input a number of statements (the Condition);
each statement has a number of arguments, which may be constants or anchored keys; and an anchored key in turn can optionally be decomposed as a pair of a Dict and a Key.
In the "original example" above, the anchored keys good_boy_issuers and receiver are not broken down, but signed_dict["friend"] is. The purpose of breaking it down, in this case, is to use an entry of a dictionary that has been signed.
In the "compiled example", all the anchored keys have been broken down into dictionaries and keys.
In general, in the front-end language, the "arguments" to an operation define a list of identifiers with types. Every statement in the "condition" must have valid arguments of the correct types: either constants, or identifiers defined in the "arguments".
In order to apply the operation, the user who wants to create a POD must give acceptable values for all the arguments. The POD prover will substitute those values for all the statements in the "Condition" and check that all substituted statements previously appear in the POD. If this check passes, the output statement is then a valid statement.
What applying the operation looks like on the back end
On the back end the "compiled example" deduction rule is converted to a sort of "template":
| Args | Condition | Output |
|---|---|---|
| ?1 (signed_dict), ?2 (signer) ?3 (good_boy_issuers_origin), ?4 (good_boy_issuers_key), ?5 (receiver_origin), ?6 (receiver_key) | SignedBy(?1, ?2), Contains(?3[?4], ?2), Equals(?1["friend"], ?5[?6]) | GoodBoy(?5[?6], ?3[?4]) |
If you want to apply this deduction rule to prove a GoodBoy statement,
you have to provide the following witnesses in-circuit.
- Copy of the deduction rule
- Values for ?1, ?2, ?3, ?4, ?5, ?6.
- Copy of the three statements in the deduction rule with ?1, ?2, ?3, ?4, ?5, ?6 filled in
- Indices of the three statements
SignedBy,Contains,Equalsin the list of previous statements.
And the circuit will verify:
- ?1, ?2, ?3, ?4, ?5, ?6 were correctly substituted into the statements
- The three statements
SignedBy,Contains,Equalsdo indeed appear at the claimed indices.
In previous versions of these docs, "operations" were called "deduction rules".
Ethdos custom predicate, using binary AND and OR: example of a recursive group
eth_dos_distance(src_or, src_key, dst_or, dst_key, distance_or, distance_key) = OR(
eth_dos_distance_ind_0(src_or, src_key, dst_or, dst_key, distance_or, distance_key),
eth_dos_distance_base(src_or, src_key, dst_or, dst_key, distance_or, distance_key)
)
eth_dos_distance_base(src_or, src_key, dst_or, dst_key, distance_or, distance_key) = AND(
Equal(src_or[src_key], dst_or[dst_key]),
ValueOf(distance_or[distance_key], 0)
)
eth_dos_distance_ind_0(src_or, src_key, dst_or, dst_key, distance_or, distance_key, private: intermed_or, intermed_key, shorter_distance_or, shorter_distance_key, one_or, one_key) = AND(
eth_dos_distance(src_or, src_key, intermed_or, intermed_key, shorter_distance_or, shorter_distance_key)
// distance == shorter_distance + 1
ValueOf(one_or[one_key], 1)
SumOf(distance_or[distance_key], shorter_distance_or[shorter_distance_key], one_or[one_key])
// intermed is a friend of dst
eth_friend(intermed_or, intermed_key, dst_or, dst_key)
)
This group includes three statements.
When the definition is serialized for hashing, the statements are renamed to SELF.1, SELF.2, SELF.3.
With this renaming and the wildcards, the first of the three definitions becomes:
SELF.1(?1, ?2, ?3, ?4, ?5, ?6) = OR(
SELF.2(?1, ?2, ?3, ?4, ?5, ?6)
SELF.3(?1, ?2, ?3, ?4, ?5, ?6)
)
and similarly for the other two definitions.
The above definition is serialized in-circuit and merkelized with a zk-friendly hash to generate the "group hash", a unique cryptographic identifier for the group.
Then the individual statements in the group are identified as:
eth_dos_distance = groupHASH.1
eth_dos_distance_base = groupHASH.2
eth_dos_distance_ind = groupHASH.3
How to hash a custom predicate
Every predicate, native or custom, is identified on the backend by a predicate ID.
The native predicates are numbered with small integers, sequentially. The ID of a custom predicate is a hash of its definition; this guarantees that two different predicates cannot have the same ID (aside from the miniscule probability of a hash collision).
This document explains in some detail how the definition of a custom predicate is serialized and hashed.
Custom predicates are defined in groups (also known as batches); see an example. The definition of a custom predicate in a group involves other predicates, which may include:
- native predicates
- previously-defined custom predicates
- other predicates in the same group.
Predicate hashing is recursive: in order to hash a group of custom predicates, we need to know IDs for all the previously-defined custom predicates it depends on.
The definition of the whole group of custom predicates is serialized (as explained below), and that serialization is hashed (using a zk-friendly hash -- in the case of the plonky2 backend, Poseidon) to give a group ID. Each predicate in the group is then referenced by
predicate_ID = (group_ID, idx)
(here idx is simply the index of the predicate in the group).
MainPOD
Introduction PODs
Introduction PODs are a kind of POD used to introduce any cryptographic data structure into the POD system. This allows the POD system to reason about cryptographic data and cryptographic primitives that are not part of the POD system itself.
An example of an IntroductionPod are the Ed25519Pod and the EcdsaPod, both
of them allowing to incorporate their respective kind of signature schemes that
are not supported in the core of the POD system.
This allows to the POD system to incorporate data validated by those
Introduction PODs, and recursively use it in future proofs combining them with
any logical reasoning together with other PODs.
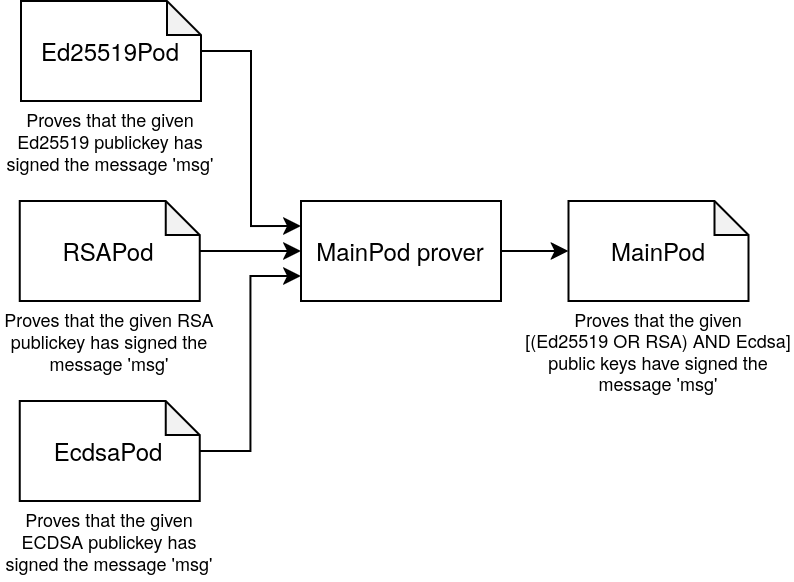
For example, we could have an scenario where we use 3 different Introduction
PODs (Ed25519Pod, RSAPod, EcdsaPod), to prove that a user controls an Ethereum
wallet AND a GitHub account. To do so, the user would produce a new MainPod
which proves that the user has signed a certain message with the given ECDSA key
(Ethereum wallet) AND with either the given Ed25519 key OR the RSA key (from
a GitHub account).
Interface
The interface of a IntroductionPod is just the one of the
Pod
trait, and by definition the IntroductionPod is expected to only output
Introduction statements (or None statements for padding).
An Introduction Statement is a Statement that uses an Introduction predicate
which embeds the verifying key of the circuit that generates it. This way the
statements generated by an IntroductionPod are self-describing.
This means that as long as we fit into the Pod interface, the
IntroductionPod will fit into the recursive verification chain of the
MainPods.
Different configurations
There are some cases, where the operations needed for the IntroductionPod
require a different circuit configuration than the standard recursive circuit
configuration that is used for the MainPods.
In those cases, we do a previous recursive step, where we verify the logic of
the intended IntroductionPod, and then the proof of this circuit is the one
verified in the real IntroductionPod.
This is done in order to be able to converge the different circuit
configuration shape (and thus different common_data) into a new proof that can
be verified with the standard configuration (used for the MainPods).
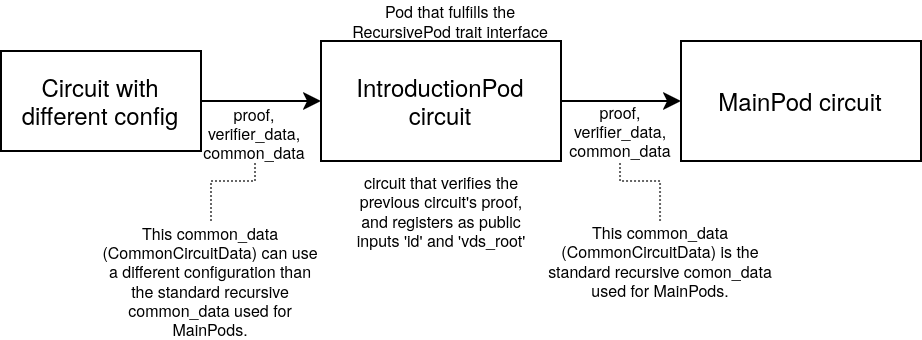
Notice that this is not a requirement for implementing a new IntroductionPod,
and if the IntroductionPod logic can be directly verified with the standard
recursion configuration, we don't need this previous recursive step.
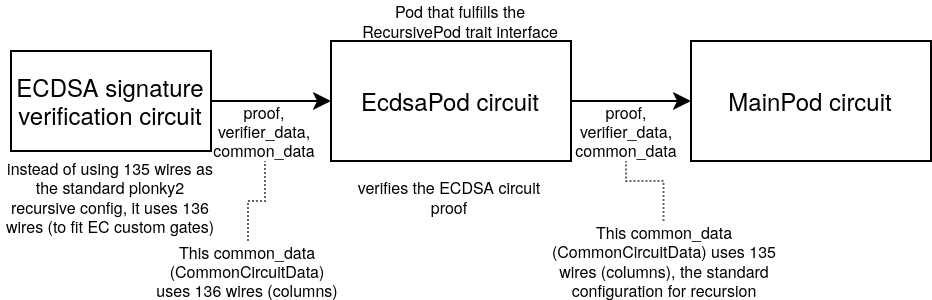
As examples of the two-recursive steps approach, we have the EcdsaPod and the
Ed25519Pod. Both of them, require different circuit configurations that would
not match the one used for the standard recursion with MainPods. Therefore we
first generate a circuit proof of correct signature verification, and then this
proof is the one actually verified in the EcdsaPod/Ed25519Pod respectively,
not the original signature itself.
Examples of
IntroductionPodscan be found at the git repository github.com/0xPARC/introduction-pods.
Examples
Examples of POD2 use cases
EthDos
Check also the custom statement example section.
Original in prolog https://gist.github.com/ludns/f84b379ec8c53c97b7f95630e16cc39c#file-eth_dos-pl
An EthDos Pod exposes a single custom statement with two custom deduction rules, the inductive case and the base case.
// src, dst: PubKey, attetation_pod: Pod
eth_dos_friend(src, dst, private: attestation_pod) = AND(
ValueOf(attestation_pod[KEY_TYPE], SIGNATURE)
Equal(attestation_pod[KEY_SIGNER], src)
Equal(attestation_pod["attestation"], dst)
)
// src, intermed, dst: PubKey, distance, shorter_distance: Int
eth_dos_distance(src, dst, distance, private: shorter_distance, intermed) = OR(
AND(
eth_dos_distance(src, intermed, shorter)
SumOf(distance, shorter_distance, 1)
eth_friend(intermed, dst)
)
AND(
Equal(src, dst)
Equal(distance, 0)
)
)
ZuKYC (classic)
Original using GPC https://github.com/proofcarryingdata/zukyc
Authority public keys:
ZOO_GOV: PubKey, issues IDsZOO_DEEL: PubKey, issues bank statements Authority lists:SANCTION_LIST: Set, Merkle Tree Root of set of sanctioned public keys- values:
["G2345678", "G1987654", "G1657678"]Date values:
- values:
NOW_MINUS_18Y: Int, 18 years agoNOW_MINUS_1Y: Int, 1 year agoNOW_MINUS_7D: Int, 7 days ago
A ZuKYC Pod exposes a single custom statement with one custom deduction rule.
// receiver: PubKey, gov_id, paystub, sk_pok: Pod, nullifier, sk: Raw
loan_check(receiver, private: gov_id, paystub, nullifier, sk, sk_pok) = AND(
Equal(gov_id["pk"], receiver)
// Not in the sanction list
SetNotContains(SANCTION_LIST, receiver)
// Valid government-issued ID
Equal(gov_id[KEY_SIGNER], ZOO_GOV)
Equal(gov_id[KEY_TYPE], SIGNATURE)
// At least 18 years old
Lt(gov_id["date_of_birth"], NOW_MINUS_18Y) # date_of_birdth is more than 18y old
Equal(paystub[KEY_SIGNER], ZOO_DEEL)
Equal(paystub[KEY_TYPE], SIGNATURE)
Equal(paystub[ssn], gov_id["ssn"])
// At least one year of consistent employment with your current employer
Lt(paystub["start_date"], NOW_MINUS_1Y) # start_date is more than 1y old
Gt(paystub["issue_date"], NOW_MINUS_7D) # issue_date is less than 7d old
// Annual salary is at least $20,000
Gt(paystub["annual_salary"], 20000)
// Private key knowledge
Equal(sk_pok[KEY_SIGNER], receiver)
Equal(sk_pok[KEY_TYPE], SIGNATURE)
Equal(sk_pok["auth"], "ZUKYC_V1_AUTH")
HashOf(, 0, sk)
// Nullifier
HashOf(nullifier, "ZUKYC_V1_NULLIFIER", sk)
)
ZuKYC (simplified for P1)
This simplified version uses less statements but requires a very similar set of features.
Authority lists:
SANCTION_LIST: Set, Merkle Tree Root of set of sanctioned public keys- values:
["G2345678", "G1987654", "G1657678"]Date values:
- values:
NOW_MINUS_18Y: Int, 18 years agoNOW_MINUS_1Y: Int, 1 year ago
A ZuKYC Pod exposes a single custom statement with one custom deduction rule.
// receiver: String, gov_pk, paystub_pk: PubKey, gov_id, paystub: Pod
loan_check(receiver, gov_pk, paystub_pk, private: gov_id, paystub) = AND(
Equal(gov_id["id_number"], receiver)
// Not in the sanction list
SetNotContains(SANCTION_LIST, gov_id["id_number"])
// Valid government-issued ID
ValueOf(gov_id[KEY_SIGNER], gov_pk)
Equal(gov_id[KEY_TYPE], SIGNATURE)
// At least 18 years old
Lt(gov_id["date_of_birth"], NOW_MINUS_18Y) # date_of_birdth is more than 18y old
ValueOf(paystub[KEY_SIGNER], paystub_pk)
Equal(paystub[KEY_TYPE], SIGNATURE)
Equal(paystub["ssn"], gov_id["ssn"])
// At least one year of consistent employment with your current employer
Lt(paystub["start_date"], NOW_MINUS_1Y) # start_date is more than 1y old
)
GreatBoy
A Good Boy Pod exposes one custom statement with one custom deduction rule.
// user: PubKey, good_boy_issuers: Set, pod: Pod, age: Int
is_good_boy(user, good_boy_issuers, private: pod, age) = AND(
Equal(pod[KEY_TYPE], SIGNATURE)
SetContains(good_boy_issuers, pod[KEY_SIGNER])
// A good boy issuer says this user is a good boy
Equal(pod["user"], user)
Equal(pod["age"], age)
)
A Friend Pod exposes one custom statement with one custom deduction rule.
// good_boy, friend: PubKey, good_boy_issuers: Set, friend_pod: Pod
is_friend(good_boy, friend, good_boy_issuers, friend_pod) = AND(
Equal(pod[KEY_TYPE], SIGNATURE)
// The issuer is a good boy
is_good_boy(good_boy, good_boy_issuers)
// A good boy says this is their friend
Equal(pod[KEY_SIGNER], good_boy)
Equal(pod["friend"], friend)
)
A Great Boy Pod exposes (in addition to the above) one new custom statement with one custom deduction rule.
great_boy: PubKey, good_boy_issuers: Set, friend_pod_0, friend_pod_1: Pod
is_great_boy(great_boy, good_boy_issuers, private: friend_pod_0, friend_pod_1) = AND
// Two good boys consider this user their friend
is_friend(friend_pod_0[KEY_SIGNER], great_boy)
is_friend(friend_pod_1[KEY_SIGNER], great_boy)
// good boy 0 != good boy 1
NotEqual(friend_pod_0[KEY_SIGNER], friend_pod_1[KEY_SIGNER])
Attested GreatBoy
An Attested Great Boy Pod is like a Great Boy Pod, but the names of the signers are revealed.
// great_boy: PubKey, friend0, friend1: String, good_boy_issuers: Set, friend_pod_0, friend_pod_1: Pod
is_great_boy(great_boy, friend0, friend1, good_boy_issuers, private: friend_pod_0, friend_pod_1) = AND
// Two good boys consider this user their friend
is_friend(friend_pod_0[KEY_SIGNER], great_boy)
is_friend(friend_pod_1[KEY_SIGNER], great_boy)
// good boy 0 != good boy 1
NotEqual(friend_pod_0[KEY_SIGNER], friend_pod_1[KEY_SIGNER])
// publicize signer names
ValueOf(friend_pod_0["name"], friend0)
ValueOf(friend_pod_1["name"], friend1)
To produce a Great Boy Pod, you need two Friend Pods, friend_pod0 and friend_pod1, each of which reveals its signer.
Tracking PodIDs: Posts and comments
The goal of this example is to model a social network, where posts and comments are pods.
A Post is a signature pod with the following fields:
content: String
poster: String
signer: PubKey
timestamp: Int
A Comment is a signature pod with the following fields:
content: String
referenced_post: PodID
signer: PubKey
timestamp: Int
A post is popular if it has at least two comments from different signers.
// post, comment1, comment2: Pod
statement is_popular(post, private: comment1, comment2) = AND(
IsEqual(comment1["referenced_post"], post)
IsEqual(comment2["referenced_post"], post)
NotEqual(comment1[KEY_SIGNER], comment2[KEY_SIGNER])
)
Multiple people over 18
Suppose I want to prove that two different people are over 18, and a third person is under 18, using the custom predicates over_18 and under_18.
// age: Int
over_18(age) = AND(
GtEq(age, 18)
)
// age: Int
under_18(age) = AND(
Lt(age, 18)
)
With wildcards:
over_18(?1) = AND(
GtEq(?1, 18)
)
Maybe I have two input pods gov_id1 and gov_id2, and I want to prove that these pods refer to two different people, both of whom are over 18; and a third pods gov_id3 refers to someone under 18. So in my public output statements, I want to have:
NotEqual(gov_id1["name"], gov_id2["name"])
over_18(gov_id1["age"])
over_18(gov_id2["age"])
under_18(gov_id3["age"]).
I would prove this with the following sequence of deductions:
| Statement | Reason |
|---|---|
| over_18(gov_id1["age"]) | over_18, ?1 = gov_id1["age"] |
| over_18(gov_id2["age"]) | over_18, ?1 = gov_id2["age"] |
| under_18(gov_id3["age"]) | under_18, ?1 = gov_id3["age"] |
| NotEqual(gov_id1["name"], gov_id2["name"]) | (not equal from entries) |
Architecture
This document explains the architecture of the current implementation.
The main logic of the POD2 implementation is divided into three modules:
- frontend
- compiles user-friendly pod declarations into intermediate representations to be consumed by the backend
- internally connects to the backend to get pods built (proved).
- presents pods to the user
- middleware
- defines the intermediate representation of Statements, Operations and interfaces of PODs
- Statements and Operations are strongly typed here
- Both frontend and backend use types defined in the middleware
- Does not import types from frontend nor backend
- backend
- takes a middleware POD request representation, signs/proves it and returns a generic POD object
If this was the Rust language compiler:
- frontend: takes a Rust code and compiles it to LLVM-IR
- middleware: defines LLVM-IR instructions and blocks
- backend: Takes LLVM-IR instructions and emits assembly code for a particular CPU
The following diagram shows visually how the components interact with each other:
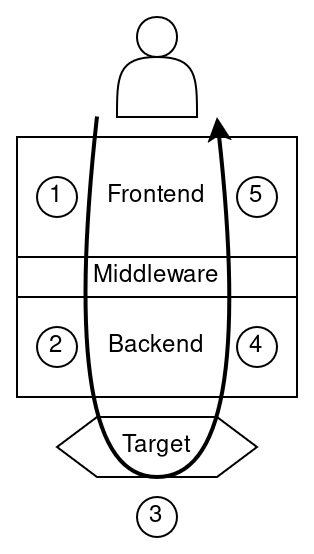
In this organization, the middleware could be defined at arbitrary points:
- closer to the user would be more high level
- closer to the target would be more low level
All these positions are OK. We just need to choose one, and we can try to choose a point that simplifies the implementation.
For example in the middleware we could define Value = 4 x Goldilock (making it slightly low level); or Value = BigUint and letting the backend choose the maximum representable value, the field encoding, etc. (making it slightly higher level).
In the current iteration we choose Value = 4 x Goldilock, but we can revisit it in a future iteration (eg. if we want to support plonky3) by either moving the middleware to a higher level, or by keeping it the same and replacing the Value definition.
The diagram above includes an arrow that would show the typical flow followed by a user making a POD. This is a simplified description of the process.
- The user interacts with the frontend API and passes a list of Operations. The frontend takes those operations and generates the corresponding Statements. The list of Operations and Statements are transformed into middleware types. This process can be seen as a compilation step. The frontend sends this middleware data as a request to the Backend.
- The backend receives a request to build a POD from a list of Statements and Operations. It takes that bundle of data and lays it out in the appropriate format to be proved by a circuit, padding unused slots, etc. Then it calls a proof system API to generate a proof.
- The target (proof system) generates a proof from some circuit description and witness data and gives it back to the backend.
- The backend receives the proof and encapsulates it in an object that adheres to the Pod trait and passes it to the frontend
- The frontend receives a "blackbox" Pod object and wraps it in a presentation layer in order to show it to the user.